Bonjour,
Imaginons que nous puissions voir les décimales d'un nombre réel comme une suite de nombres dont l'ensemble des valeurs de la suite est

et ou chacune de ces décimales possède un rang (le rang

est attribué à la première décimale, le rang

est attribué à la deuxième décimale etc...)
Il s'en suit qu'à chaque réel
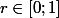
, je peux ainsi associer une suite de nombres rangés du rang

, au rang

.
Par exemple, la constante Oméga :

est ainsi associée à la suite de nombres
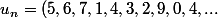)
Imaginons à présent qu'à chacun des termes
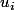
de cette suite on fasse correspondre le terme
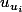
. Nous créons alors une seconde suite

engendrée par

et telle que chacun des termes
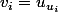
.
Il est alors possible de déterminer chacun des termes
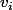
de la suite

:
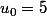
et on fait correspondre au nombre

le terme
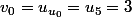
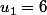
et on fait correspondre au nombre

le terme
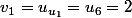
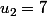
et on fait correspondre au nombre

le terme
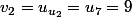
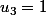
et on fait correspondre au nombre

le terme
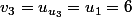
...
La suite engendrée par
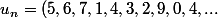)
est donc
)
Il est alors possible d'associer à la suite

un réel
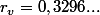 Pour corser l'affaire, je fixe deux règles supplémentaires :1/
Pour corser l'affaire, je fixe deux règles supplémentaires :1/ Tout terme
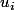
de la suite

ne peut servir qu'une seule et unique fois pour engendrer un terme
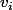
de la suite

. Lorsque le terme
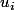
à été utilisé, le terme
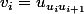
exemple :
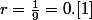
est associé à la suite
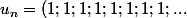)
Il est possible de déterminer chacun des termes
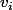
de la suite

ainsi :
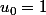
appelle le terme de rang

à savoir
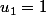
donc
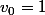
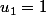
appelle le terme de rang

mais ce terme à déjà été utilisé donc l'appel se fait sur le terme de rang
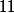
(concaténation de
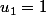
et de
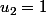
) à savoir
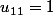
donc
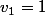
mais
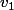
à été engendré par le terme
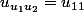
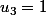
appelle le terme de rang

mais ce terme à déjà été utilisé donc l'appel se fait sur le terme de rang
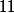
mais ce terme à déjà été utilisé également donc l'appel se fait sur le terme de rang
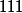
(concaténation de
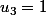
et
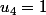
et
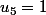
) à savoir
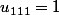
donc
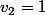
mais
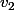
à été engendré par le terme
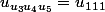 2/
2/ Tout nombre décimal
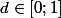
servant de base pour créer la suite

ne sera jamais écrit sous la forme d'un développement décimal impropre
exemple :
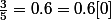
mais ne s'écrira jamais sous la forme impropre :
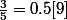
Dans la pratique, la détermination des termes de la suite

se fait directement à partir de la lecture des décimales du réel

auquel on associe la suite

.
Exemples :1) 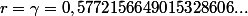
En lisant de gauche à droite les décimales du réel, il vient :

appelle la 6eme décimale à savoir


appelle la 8eme décimale à savoir

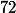
appelle la 73eme décimale à savoir


appelle la 2eme décimale à savoir

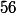
appelle la 57eme décimale à savoir


appelle la 7eme décimale à savoir


appelle la 5eme décimale à savoir


appelle la 10eme décimale à savoir


appelle la 1ere décimale à savoir

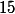
appelle la 16eme décimale à savoir
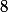
...
La suite
)
à laquelle j'associe le réel
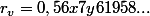 2)
2) 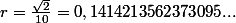
En lisant de gauche à droite les décimales du réel, il vient :

appelle la 2e décimale à savoir


appelle la 5e décimale à savoir

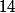
appelle la 15e décimale à savoir


appelle la 3e décimale à savoir

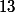
appelle la 14e décimale à savoir


appelle la 6e décimale à savoir


appelle la 7e décimale à savoir

...
La suite
)
à laquelle j'associe le réel
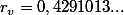
Il est donc possible (avec les règles données ci-dessus) de transformer un nombre réel
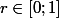
en un nombre réel
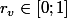
. Cette transformation (opération) sera notée
# et définie sur l'intervalle
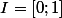
Mais s'il est possible d'appeler les décimales d'un réel

dans l'ordre de ses propres décimales, il est également possible d'appeler les décimales d'un réel

dans l'ordre des décimales d'un autre réel

.
Dans tous les exemples précédents le réel

de sorte que l'opérande appelant était la même que l'opérande appelé :
 #
#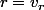
Prenons l'exemple de deux opérandes

et

inégaux et appelons
# l'opération consistant à transformer les décimales de

dans l'ordre de

. Une telle opération sera notée
 #
#
avec

l'opérande appelant et

l'opérande appelé.
Par convention, tout opérande positionné à gauche de l'opération
# est l'opérande appelant et tout opérande positionné à droite de l'opération
# est l'opérande appelé :
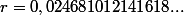
(opérande appelant dont les décimales forment la suite des nombres pairs)
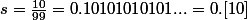
(opérande appelé)
 #
#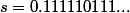
Si le résultat d'une telle opération donne nécessairement un nombre appartenant à l'intervalle unité
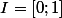
alors l'opération
# constitue une loi de composition interne dans la mesure ou elle associe à deux éléments de

un élément de ce même ensemble

.
Le couple
(I,#) serait alors par définition un magma dont les propriétés restent à explorer
 En espérant ne pas avoir écrit trop de bêtises, n'hésitez pas à me corriger ou à me solliciter sur certains points que j'ai mal rédigé.
En espérant ne pas avoir écrit trop de bêtises, n'hésitez pas à me corriger ou à me solliciter sur certains points que j'ai mal rédigé.