Paradoxe de Simpson (2e partie)
28 messages
- Page 1 sur 2 - 1, 2
Paradoxe de Simpson (2e partie)
Paradoxe de Simpson
Dans une classe de 31 élèves, on propose un examen de fin d'année en maths, avec 2 sujets au choix : le sujet A et le sujet B.
Voici les résultats de réussite en fonction des sujets A et B et du sexe des candidats :
Il est clair que les filles ont bien mieux réussi que les garçons.
Mais est-ce le sujet A ou le sujet B qui a été le mieux réussi ?
Première question
Vous êtes un(e) de ces candidat pris au hasard (fille ou garçon, on ne sait pas).
Faut-il mieux avoir choisi le sujet A ou le sujet B ?
Deuxième question
Vous êtes un garçon.
Faut-il mieux avoir choisi le sujet A ou le sujet B ?
Troisième question
Vous êtes une fille.
Faut-il mieux avoir choisi le sujet A ou le sujet B ?
Quatrième question : conclusion
Alors, finalement, faut-il mieux avoir choisi le sujet A ou le sujet B ?
Dans une classe de 31 élèves, on propose un examen de fin d'année en maths, avec 2 sujets au choix : le sujet A et le sujet B.
Voici les résultats de réussite en fonction des sujets A et B et du sexe des candidats :
Il est clair que les filles ont bien mieux réussi que les garçons.
Mais est-ce le sujet A ou le sujet B qui a été le mieux réussi ?
Première question
Vous êtes un(e) de ces candidat pris au hasard (fille ou garçon, on ne sait pas).
Faut-il mieux avoir choisi le sujet A ou le sujet B ?
Deuxième question
Vous êtes un garçon.
Faut-il mieux avoir choisi le sujet A ou le sujet B ?
Troisième question
Vous êtes une fille.
Faut-il mieux avoir choisi le sujet A ou le sujet B ?
Quatrième question : conclusion
Alors, finalement, faut-il mieux avoir choisi le sujet A ou le sujet B ?
Modifié en dernier par Rhambo le 29 Mai 2016, 10:08, modifié 1 fois.
Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
Je sais que le paradoxe de Simpson se produit lorsqu'il y a un facteur de confusion, autrement dit, dans le cas qui nous occupe, une corrélation entre le sexe d'un candidat et le choix du sujet, A ou B.
Cependant, j'ai construit mon exemple complètement artificiellement, à partir de ce graphique que j'ai réalisé sous Cabri :
En gros, dans cet exemple, j'ai trouvé des fractions telles que :
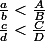 mais :
mais : 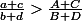
Ici :
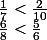 mais :
mais : 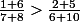 puisque de façon triviale :
puisque de façon triviale : 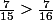
Donc bien malin celui qui pourrait imaginer un facteur de confusion rationnel qui expliquerait le paradoxe.
Car mon découpage garçons/filles est totalement arbitraire (j'ai inventé mon exemple), et j'aurais peut-être pu trouver un autre découpage qui rend le sujet A plus favorable aux candidats des deux sous groupes.
Par exemple : ceux dont le nom de famille commence par une lettre dans la première moitié de l'alphabet [de A à M], et ceux dont l'initiale du nom est dans la deuxième moitié de l'alphabet [de N à Z], ou n'importe quel autre découpage de la classe en deux sous-groupe judicieusement choisis.
Ma question est donc :
"Un tel découpage (qui rend le sujet A plus favorable aux candidats des deux sous-groupes) est-il possible ? "
et si oui, donnez-moi un exemple (qui respecte mes données : 31 candidats, 15 sujets A choisis dont 7 qui le réussissent, 16 sujets B choisis dont 7 qui le réussissent).
Cependant, j'ai construit mon exemple complètement artificiellement, à partir de ce graphique que j'ai réalisé sous Cabri :
En gros, dans cet exemple, j'ai trouvé des fractions telles que :
Ici :
Donc bien malin celui qui pourrait imaginer un facteur de confusion rationnel qui expliquerait le paradoxe.
Car mon découpage garçons/filles est totalement arbitraire (j'ai inventé mon exemple), et j'aurais peut-être pu trouver un autre découpage qui rend le sujet A plus favorable aux candidats des deux sous groupes.
Par exemple : ceux dont le nom de famille commence par une lettre dans la première moitié de l'alphabet [de A à M], et ceux dont l'initiale du nom est dans la deuxième moitié de l'alphabet [de N à Z], ou n'importe quel autre découpage de la classe en deux sous-groupe judicieusement choisis.
Ma question est donc :
"Un tel découpage (qui rend le sujet A plus favorable aux candidats des deux sous-groupes) est-il possible ? "
et si oui, donnez-moi un exemple (qui respecte mes données : 31 candidats, 15 sujets A choisis dont 7 qui le réussissent, 16 sujets B choisis dont 7 qui le réussissent).
Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
Désolé, je me suis encore un peu trompé, ce post aurait dû faire partie du forum "Salon Mathématiques", et pas "Collège et Primaire", mais je ne sais pas déplacer un sujet...
Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
salut
je pense que pour avoir différentes variantes l'utilisation d'un tableur te permettrait de voir et faire varier les différents effectifs des filles/garçons et des réussite/non réussite ....
ou de fixer certains paramètres et de constater ce qui se passe ....
ainsi par exemple ici tu as presque autant de filles que de garçons mais si tu as une proportion 1/3 2/3 par exemple que se passe-t-il ....
je pense que pour avoir différentes variantes l'utilisation d'un tableur te permettrait de voir et faire varier les différents effectifs des filles/garçons et des réussite/non réussite ....
ou de fixer certains paramètres et de constater ce qui se passe ....
ainsi par exemple ici tu as presque autant de filles que de garçons mais si tu as une proportion 1/3 2/3 par exemple que se passe-t-il ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Paradoxe de Simpson (2e partie)
"Donc bien malin celui qui pourrait imaginer un facteur de confusion rationnel qui expliquerait le paradoxe."
je n'ai pas compris ta démarche.
tu pars de données objectives = des rapports de fraction qui font que somme des numérateurs sur somme des dénominateurs inverse les inégalités de fraction
sur ces rapports de fraction tu plaques un exemple possible fille garçon réussite ou non à un examen. Ce truc là est inventé, donc comment il pourrait y avoir un facteur de confusion rationnel?
pas bien compris ton interrogation
je n'ai pas compris ta démarche.
tu pars de données objectives = des rapports de fraction qui font que somme des numérateurs sur somme des dénominateurs inverse les inégalités de fraction
sur ces rapports de fraction tu plaques un exemple possible fille garçon réussite ou non à un examen. Ce truc là est inventé, donc comment il pourrait y avoir un facteur de confusion rationnel?
pas bien compris ton interrogation
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Paradoxe de Simpson (2e partie)
Je suis bien d'accord avec toi, Beagle : j'ai effectivement inventé ma situation (mais elle pourrait néanmoins être un vrai résultat, je veux dire un résultat qui correspondrait à une vraie mise en situation).
C'est bien pour ça que je dis qu'il ne peut pas y avoir de facteur de confusion ("bien malin celui qui...") puisqu'un facteur de confusion serait une explication causale dans une situation bien réelle.
Mais alors du coup, dans mon cas de figure, peut-on répondre à la question :
"Lequel des deux sujet A ou B a-t-il été le mieux réussi ? "
Se peut-il qu'en raison du paradoxe de Simpson, il n'y ait pas de réponse à cette question ?
Si on ne considère pas le sexe des élèves, c'est le sujet A qui a été le mieux réussi, mais en revanche, aussi bien les garçons que les filles ont mieux réussi le sujet B. Je n'arrive pas à décider quelle est la bonne réponse.
Ça bouleverserait alors un peu mes convictions de matheux, car d'une manière générale, j'ai l'intuition que deux grandeurs mesurables de même nature sont comparables...
C'est bien pour ça que je dis qu'il ne peut pas y avoir de facteur de confusion ("bien malin celui qui...") puisqu'un facteur de confusion serait une explication causale dans une situation bien réelle.
Mais alors du coup, dans mon cas de figure, peut-on répondre à la question :
"Lequel des deux sujet A ou B a-t-il été le mieux réussi ? "
Se peut-il qu'en raison du paradoxe de Simpson, il n'y ait pas de réponse à cette question ?
Si on ne considère pas le sexe des élèves, c'est le sujet A qui a été le mieux réussi, mais en revanche, aussi bien les garçons que les filles ont mieux réussi le sujet B. Je n'arrive pas à décider quelle est la bonne réponse.
Ça bouleverserait alors un peu mes convictions de matheux, car d'une manière générale, j'ai l'intuition que deux grandeurs mesurables de même nature sont comparables...
Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
Bah c'est le sujet A qui est le mieux réussi,
alors que B est mieux réussi par les deux groupes,
c'est ça qui est super.Le principe d'un paradoxe c'est de te filer le vertige.
Mais prends des nombres plus simples,
admettons un groupe qui aurait 1/1 de réussite, tu le compares à (n-1)/n il est gagnant ce groupe de 1/1,
pourtant (n-1)/n c'est du costaud (et n-1 en réussite en nombre absolu versus 1 ça fait réver !)
Alors en regard de cela tu compares du 1/2 avec du (n-k)/(n+1):
(n-1)/n ........... 1/1
1/2...................(n-k)/(n+1)
-----------------------------
n/(n+2) .......(n-k+1)/(n+2)
c'est assez fastoche de faire mieux que 1/2 avec du (n-k)/(n+1)
et on voit bien au final que c'est n qui sera sup à (n-k+1)
On n'additionne pas des fractions de même dénominateur, l'addition de fractions de dénominateur différent c'est champion pour dire à l'avance plus grand ou plus petit, ça se joue des fois à rien du tout ...
alors que B est mieux réussi par les deux groupes,
c'est ça qui est super.Le principe d'un paradoxe c'est de te filer le vertige.
Mais prends des nombres plus simples,
admettons un groupe qui aurait 1/1 de réussite, tu le compares à (n-1)/n il est gagnant ce groupe de 1/1,
pourtant (n-1)/n c'est du costaud (et n-1 en réussite en nombre absolu versus 1 ça fait réver !)
Alors en regard de cela tu compares du 1/2 avec du (n-k)/(n+1):
(n-1)/n ........... 1/1
1/2...................(n-k)/(n+1)
-----------------------------
n/(n+2) .......(n-k+1)/(n+2)
c'est assez fastoche de faire mieux que 1/2 avec du (n-k)/(n+1)
et on voit bien au final que c'est n qui sera sup à (n-k+1)
On n'additionne pas des fractions de même dénominateur, l'addition de fractions de dénominateur différent c'est champion pour dire à l'avance plus grand ou plus petit, ça se joue des fois à rien du tout ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Paradoxe de Simpson (2e partie)
peut-être pour éclairer la situation on peut regarder des "probabilités conditionnelles"
un élève a réussi ; quelle est la probabilité que ce soit une fille ? un garçon ?
un élève a réussi ; quelle est la probabilité qu'il ai réussi le sujet A?
1 F (1 G) a réussi ; quelle est la probabilité qu'elle (qu'il) ait réussi le sujet A ?
....
un élève a réussi ; quelle est la probabilité que ce soit une fille ? un garçon ?
un élève a réussi ; quelle est la probabilité qu'il ai réussi le sujet A?
1 F (1 G) a réussi ; quelle est la probabilité qu'elle (qu'il) ait réussi le sujet A ?
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Paradoxe de Simpson (2e partie)
Rhambo a écrit:Je n'arrive pas à décider quelle est la bonne réponse.
Ça bouleverserait alors un peu mes convictions de matheux, car d'une manière générale, j'ai l'intuition que deux grandeurs mesurables de même nature sont comparables...
Bonsoir,
Les garçons et les filles individuellement ont mieux réussi le sujet B. Mais comme les filles ont choisi le sujet A dans une proportion plus grande (8/15), que les garçons (6/16), et qu'elles ont mieux réussi dans l'ensemble que les garçons, le sujet A a été globalement mieux réussi que le sujet B.
Pour moi, il n'y a pas de paradoxe. Tout dépend du contexte (en terme de probabilités, de l'univers) dans lequel on se trouve : la probabilité de réussir le sujet A (dans l'univers garçons + filles) est différente de la probabilité de réussir le sujet sachant que l'on est une fille... ou que l'on est un garçon... (probabilité conditionnelle).
Modifié en dernier par Pseuda le 30 Mai 2016, 12:48, modifié 2 fois.
Re: Paradoxe de Simpson (2e partie)
beagle a écrit:c'est ça qui est super.Le principe d'un paradoxe c'est de te filer le vertige.
Bah, ok, mais autant les paradoxes style menteur ou Achille, je m'étais habitué depuis tout petit (ça me semble même plus très intéressant). Mais découvrir à 45 balais qu'avec des toutes bêtes fractions de niveau 5e, je peux être tout chamboulé dans mes croyances, ça craint !

Par contre ça me donne des idées pour illustrer mon cours sur les fractions, mais je sais pas si je dois : les élèves ont déjà assez de "facteurs de confusion" dans leur tête pour leur en rajouter encore... est-ce que c'est très prudent ?!!!
Pour ton exemple avec les (n-k)/n+1, j'avoue que je n'ai rien compris, je verrai ça à tête reposée avec un papier et un crayon (t'as l'air de suggérer qu'avec n'importe quel groupe, on peut toujours le subdiviser en sous groupes pour tomber dans le paradoxe de Simpson, mais j'ai pas vraiment saisi la logique - je ne suis qu'un petit prof de maths de rien du tout, héhéhé
 ).
).Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
J'ai juste choisi des exemples assez faciles et extrêmes vu que perso je suis aussi très limité:
1/1 je suis assez à l'aise à comparer à du (n-1)/n j'arrive à suivre c'est plus petit en % de réussite, mais en effectif de réussite cela fait facilement pencher dans la balance on aura du (n-1) effectif versus un pauvre 1,
construire une seconde ligne avec ça c'est du gateau (normal pour les fractions),
j'ai mis du 1/2 pour pas trop faire monter les effectifs mais dans cette case j'aurai pu mettre du 1/3 du 1/4, toutes choses faciles à battre en fraction de l'autre coté ...
1/1 je suis assez à l'aise à comparer à du (n-1)/n j'arrive à suivre c'est plus petit en % de réussite, mais en effectif de réussite cela fait facilement pencher dans la balance on aura du (n-1) effectif versus un pauvre 1,
construire une seconde ligne avec ça c'est du gateau (normal pour les fractions),
j'ai mis du 1/2 pour pas trop faire monter les effectifs mais dans cette case j'aurai pu mettre du 1/3 du 1/4, toutes choses faciles à battre en fraction de l'autre coté ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Paradoxe de Simpson (2e partie)
Rhambo a écrit:Par contre ça me donne des idées pour illustrer mon cours sur les fractions, mais je sais pas si je dois : les élèves ont déjà assez de "facteurs de confusion" dans leur tête pour leur en rajouter encore... est-ce que c'est très prudent ?!!!
Cela ne me paraît pas très prudent en effet. Ils ont déjà suffisamment de mal à comprendre les fractions ....
Re: Paradoxe de Simpson (2e partie)
Ma question ultime, en fin de compte, c'est :
Etant données deux fractions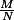 et
et 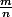 telles que
telles que 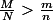
peut-on toujours trouver quatre fractions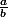 ,
,  ,
, 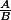 ,
, 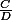
avec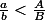 et
et 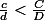
et telles que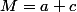 ,
, 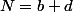 ,
, 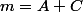 et
et 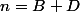 ?
?
Ce qui revient à dire (mais je me trompe peut-être dans mes équivalences) :
Etant donné un groupe dont on étudie deux caractéristiques Q et q (dont l'une est prédominante, par exemple Q), on peut toujours trouver une subdivision de notre groupe en deux sous-groupes complémentaires pour laquelle c'est la caractéristique q qui l'emporte (dans chacun des deux sous-groupes).
Attention : je me plante peut-être complètement... Je n'ai pas la prétention d'affirmer que ces deux propositions sont vraies ! Je ne suis même pas sûr qu'elles soient équivalentes...
Etant données deux fractions
peut-on toujours trouver quatre fractions
avec
et telles que
Ce qui revient à dire (mais je me trompe peut-être dans mes équivalences) :
Etant donné un groupe dont on étudie deux caractéristiques Q et q (dont l'une est prédominante, par exemple Q), on peut toujours trouver une subdivision de notre groupe en deux sous-groupes complémentaires pour laquelle c'est la caractéristique q qui l'emporte (dans chacun des deux sous-groupes).
Attention : je me plante peut-être complètement... Je n'ai pas la prétention d'affirmer que ces deux propositions sont vraies ! Je ne suis même pas sûr qu'elles soient équivalentes...

Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
Bonjour,
Il me semble que le paradoxe de Simson est habituellement cité quand par exemple, deux catégories différentes d'employés ont un salaire moyen pour chaque catégorie, plus élevé dans une entreprise A que dans une entreprise B, mais que globalement (les deux catégories confondues), leur salaire moyen est plus élevé dans l'entreprise B que dans l'entreprise A.
A mon avis, tu pourrais dans le même registre, à la fois généraliser et simplifier ton problème, en considérant des notes moyennes (plutôt que des taux de réussite, mais cela marche aussi) obtenues aux sujets A et B pour les filles et les garçons.
Par exemple :
x = note moyenne des garçons au sujet A (ici taux de réussite 1/7)
y = note moyenne des filles au sujet A (ici 6/8)
z = note moyenne des garçons au sujet B (ici 2/10)
t = note moyenne des filles au sujet B (ici 5/6)
On a : 0 x
x  z, et 0
z, et 0  y
y  t et on cherche une proportion p (ici 7/15 : proportion de garçons parmi les élèves qui ont choisi le sujet A) et q (ici 10/16 : B) telle que p*x + (1-p)*y
t et on cherche une proportion p (ici 7/15 : proportion de garçons parmi les élèves qui ont choisi le sujet A) et q (ici 10/16 : B) telle que p*x + (1-p)*y  q*z + (1-q) * t.
q*z + (1-q) * t.
On obtient ici : 7/15 7/16.
7/16.
Le problème est comment doivent être x, y , z et t, pour qu'il existe p et q qui vérifient la dernière inéquation.
Tu peux maintenant remplacer toutes ces lettres par des fractions, mais à mon avis cela complique inutilement.
Il me semble que le paradoxe de Simson est habituellement cité quand par exemple, deux catégories différentes d'employés ont un salaire moyen pour chaque catégorie, plus élevé dans une entreprise A que dans une entreprise B, mais que globalement (les deux catégories confondues), leur salaire moyen est plus élevé dans l'entreprise B que dans l'entreprise A.
A mon avis, tu pourrais dans le même registre, à la fois généraliser et simplifier ton problème, en considérant des notes moyennes (plutôt que des taux de réussite, mais cela marche aussi) obtenues aux sujets A et B pour les filles et les garçons.
Par exemple :
x = note moyenne des garçons au sujet A (ici taux de réussite 1/7)
y = note moyenne des filles au sujet A (ici 6/8)
z = note moyenne des garçons au sujet B (ici 2/10)
t = note moyenne des filles au sujet B (ici 5/6)
On a : 0
On obtient ici : 7/15
Le problème est comment doivent être x, y , z et t, pour qu'il existe p et q qui vérifient la dernière inéquation.
Tu peux maintenant remplacer toutes ces lettres par des fractions, mais à mon avis cela complique inutilement.
Re: Paradoxe de Simpson (2e partie)
Oui, en évitant les fractions, ça réduit déjà par deux le nombre de variables, et donc d'inconnues 
Je me penche sur le problème dès que j'ai fini mes paquets de copies (heureusement qu'en vrai, je n'ai pas fait deux sujets A et B pour mon interro !!!
 )
)
Je me penche sur le problème dès que j'ai fini mes paquets de copies (heureusement qu'en vrai, je n'ai pas fait deux sujets A et B pour mon interro !!!

 )
)Philippe (prof en collège)
Re: Paradoxe de Simpson (2e partie)
Bonsoir,
En fait je me rends compte que ton problème est inverse : tu connais 2 nombres u et v avec u v
v  0, et tu te demandes s'il existe 4 nombres x, y, z, t
0, et tu te demandes s'il existe 4 nombres x, y, z, t  0, et 2 proportions p et q
0, et 2 proportions p et q  [0 ; 1] tels que 0
[0 ; 1] tels que 0  x
x  z, et 0
z, et 0  y
y  t , et u=p*x + (1-p)*y , v=q*z + (1-q)*t.
t , et u=p*x + (1-p)*y , v=q*z + (1-q)*t.
Sauf que là, il faut rajouter comme contrainte supplémentaire pour ton problème, que x, y, z, t, p et q soient des rationnels.
Bon courage !
En fait je me rends compte que ton problème est inverse : tu connais 2 nombres u et v avec u
Sauf que là, il faut rajouter comme contrainte supplémentaire pour ton problème, que x, y, z, t, p et q soient des rationnels.
Bon courage !
Re: Paradoxe de Simpson (2e partie)
La contrainte la plus forte me semble être celle ci :
a/b < (a+1)/(b+1) pour a < b
Dans ce cas, on peut faire :
a / b = 3 / 1 + (a-3) / (b-1)
(a+1) / (b+1) = 5 / 2 + (a-4) / (b-1)
Il faut alors juste que a >= 5 et b >= 6.
a/b < (a+1)/(b+1) pour a < b
Dans ce cas, on peut faire :
a / b = 3 / 1 + (a-3) / (b-1)
(a+1) / (b+1) = 5 / 2 + (a-4) / (b-1)
Il faut alors juste que a >= 5 et b >= 6.
Re: Paradoxe de Simpson (2e partie)
Rhambo a écrit:Ma question ultime, en fin de compte, c'est :
Etant données deux fractionset
telles que
peut-on toujours trouver quatre fractions,
,
,
avecet
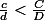
et telles que,
,
et
?
Bonsoir,
Etant donné que pour tous a, b, c et d positifs :
Si toutes les fractions sont < à 1, cette condition nécessaire paraît suffisante (
Modifié en dernier par Pseuda le 01 Juin 2016, 12:44, modifié 1 fois.
Re: Paradoxe de Simpson (2e partie)
L'utilisation des fractions cache peut-être un peu le phénomène très simple :
On peut avoir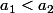 et
et 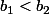 , et en même temps une moyenne pondérée
, et en même temps une moyenne pondérée b_1) strictement plus grande que
strictement plus grande que b_2) (avec
(avec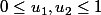 ).
).
Il faut et il suffit que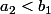 ou
ou 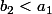 pour qu'on puisse fabriquer une moyenne pondérée de
pour qu'on puisse fabriquer une moyenne pondérée de  et
et  plus grande qu'une moyenne pondérée de
plus grande qu'une moyenne pondérée de 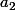 et
et 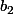 (les poids ne sont bien entendu pas les mêmes dans les deux cas).
(les poids ne sont bien entendu pas les mêmes dans les deux cas).
On peut avoir
Il faut et il suffit que
Re: Paradoxe de Simpson (2e partie)
Bonsoir,
Un (bon) résumé de la situation concernant le paradoxe de Simpson :
http://www.lifl.fr/~jdelahay/pls/236.pdf
Un (bon) résumé de la situation concernant le paradoxe de Simpson :
http://www.lifl.fr/~jdelahay/pls/236.pdf
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
