Barycentres, prouver un alignement de points

[skater41]

Bonjour, je suis actuellement en 1S, et j'ai un DM à faire pour mercredi en raison de la neige qui nous empêche l'accès au lycée. J'ai donc reçu le sujet par internet sans d'autres explications.

ABC est un triangle, O est le milieu de [BC] et J celui de [AC].

I est le barycentre des points (A,2) et (B,1).

K est le barycentre de (I,3) et (J,2).

Montrer que les points A, K et O sont alignés. :triste:

J'ai commencé par calculer les deux barycentres que j'ai placé sur le triangle ABC. On voit que les points A, K et O sont alignés, mais je ne sais pas comment le prouver, j'ai recherché un peu sur internet, et les gens conseillent d'utiliser la propriété partiel du barycentre, seulement voilà, je ne sais pas ce que c'est, et encore moins comment l'utiliser... C'est la bonne technique ? Si oui, comment l'utiliser ?

Je vous remercie d'avance si vous pouvez m'aider. Bonne journée :we:

[Sa Majesté]

Salut

Si tu as vu les barycentres tu dois savoir que I barycentre des points (A,2) et (B,1) peut s'exprimer vectoriellement par



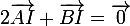
Écris les 4 égalités vectorielles qui traduisent l'énoncé et en les triturant avec la relation de Chasles tu trouveras une relation vectorielle liant A, K et O qui montrera que les points sont alignés

[skater41]

Merci, ça m'a déjà pas mal aidé, mais ce que je ne comprends pas, c'est comment mettre en relation, après avoir utilisé la relation de Chasles, pour trouver une relation avec A, K et O, il faut trouver une relation du style, ? La relation n'est certainement pas la bonne c'est juste un exemple

[Sa Majesté]

Oui c'est ça
Quelles sont les égalités que tu peux déjà écrire ?

[skater41]

Alors j'ai:









J'ai appliqué Chasles sur chacun d'eux, mais je trouve des relations qui n'ont aucun rapport les unes avec les autres.

[Sa Majesté]

OK alors prends la 2ème par exemple
Tu sais qu'à la fin il faut trouver une relation avec A, O et K seulement
Dans la 2ème tu n'as que du K donc il faut utiliser Chasles en introduisant A et O
Par ex


Comme ça tu obtiens du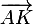 ce qui est bien
Ensuite il faut continuer à triturer en t'aidant des égalités 1, 3 et 4

[skater41]

Je dois rester sur la même équation ou bien en prendre une autre et y introduire 0 comme tu l'a fait avec A ?

[Sa Majesté]

Non reste sur la même
Évidemment il ne faut plus toucher à sinon tu vas tourner en rond
Remplace et

[skater41]

En fait, il faut que j'arrive à enlever le I et le J ?

[Sa Majesté]

Oui c'est ça
Aide-toi des relations 1 et 4 pour ça

[skater41]

Mais si j'utilise ces relations, je vais sûrement enlever le I et le J, mais à la place j'introduirai un B et un C :hum:

EDIT: Ah oui mais après je n'aurais qu'a utiliser la relation 3, et BO + CO = vecteur nul !

Est-ce bien ça ?

[Sa Majesté]

Oui c'est ça

[skater41]

Merci beaucoup j'ai réussi à finir l'exercice grâce à ton aide :we:

[Sa Majesté]

De rien, bonne continuation ! :zen: