Aide compréhension polynômes

[matelos90]

Bonjour quelqu'un pourrait il m'expliquer cette exercice , je ne comprends rien ...

On considère le polynôme défini par p (X) =X^5-5X^4+7X^3-2X^2+4X-8

1 calculer les polynômes dérivés d'ordre 1, 2, 3 de p . En déduire que 2 est racine triple de p
2 déterminer toutes les racines de p et préciser leurs ordres de multiplicité
3 écrire la décomposition de p en facteurs irreductibles dans l'ensemble des complexes puis dans lensemble des réels.

Merci d'avance pour vos réponses .

[Carpate]

Bonjour quelqu'un pourrait il m'expliquer cette exercice , je ne comprends rien ...

On considère le polynôme défini par p (X) =X^5-5X^4+7X^3-2X^2+4X-8

1 calculer les polynômes dérivés d'ordre 1, 2, 3 de p . En déduire que 2 est racine triple de p
2 déterminer toutes les racines de p et préciser leurs ordres de multiplicité
3 écrire la décomposition de p en facteurs irreductibles dans l'ensemble des complexes puis dans lensemble des réels.

Merci d'avance pour vos réponses .

Si tu postes dans le rubrique "Forum Supérieur", j'imagine que tu sais dériver une fonction polynomiale. Qu'obtiens-tu pour les dérivées successives de p(X) ?

[matelos90]

Ce que je ne comprends pas c'est qu'on me dit calculer les polynômes dérivés d'ordre 1, 2, 3 de p . Ca veut dire je dois dériver que 7x^3 , -2x^2, +4x ? Ou tout ? Ce qui me derange c'est " ordre 1, 2, 3 "

[matelos90]

Il faut faire trois fois la dérivé de p ?
J'essaie de comprendre ...

[Carpate]

Ce que je ne comprends pas c'est qu'on me dit calculer les polynômes dérivés d'ordre 1, 2, 3 de p . Ca veut dire je dois dériver que 7x^3 , -2x^2, +4x ? Ou tout ? Ce qui me derange c'est " ordre 1, 2, 3 "

Le polynôme dérivée d'ordre n de P(x) noté s'obtient en dérivant successivement (donc n fois) le polynôme P(x)

[matelos90]

D'accord ici n=3 j'obtiens 60x^2-60x+42
C'est cela ?

[Archibald]

Tu pourrais nous développer le calcul de tes trois dérivées, stp ?

[matelos90]

Oula ca veut dire que c'est pas ça ...
Désolée je suis pas très forte en maths .

Je dérive une première fois ca donne 5x^4-20x^3+21x^2-4x+4
Je derive la formule au dessus 20x^3-30x^2+42x-4
Et la 3eme fois on a 60x^2-60x+42 ...

[Carpate]

Oula ca veut dire que c'est pas ça ...
Désolée je suis pas très forte en maths .

Je dérive une première fois ca donne 5x^4-20x^3+21x^2-4x+4
Je derive la formule au dessus 20x^3-30x^2+42x-4
Et la 3eme fois on a 60x^2-60x+42 ...

[matelos90]

Mais faut la dérivé 3 fois donc il faut continuer non?

[Archibald]

Oula ca veut dire que c'est pas ça ...

Absolument pas. C'était juste pour vérifier si les dérivées d'ordre 1 et 2 étaient correctes.

Ok pour mais pour , il y a une erreur sur le coefficient de )

Une fois cela corrigé, tu pourras dériver pour obtenir .

[matelos90]

A oui en effet j'avais pas vu .

[matelos90]

Par contre pour trouver la racine triple de p on fait delta ? Cqr j arrive pas a trouvé 2

[Carpate]

Par contre pour trouver la racine triple de p on fait delta ? Cqr j arrive pas a trouvé 2

P(2)=P'(2)=P''(2)=0
L'exercice veut te faire "toucher du doigt" que si un réel est racine d'un polynôme et de ses 2 premières dérivées, ce nombre est racine triple du polynôme
où Q_2(x) est un polynôme de degré 2 de la forme
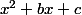
P(x) s'écrit car
Les coefficients b et c de ce polynôme peuvent s'obtenir de 2 façons :
1) identifier P(x) au polynôme obtenu en effectuant le produit
2) effectuer la division euclidienne de P(x) par

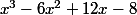
[matelos90]

Daccord je te remercie je vais essayer de le faire et voir si je trouve pareil . Merci pour votre patience .

[Carpate]

Daccord je te remercie je vais essayer de le faire et voir si je trouve pareil . Merci pour votre patience .

Tu devrais aboutir à
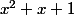
Et se factorise sur en ...

[Azarnok]

Salut Carpate,

A la fin, de la division j’aboutis à P(x)=((x-2)^3)(x^2-11X+85)+(-636X^2+936X+672).
Et je n'arrive pas à trouver mon erreur, pourrais-tu m'aider à la trouver ?

[matelos90]

C est normal il sait tromper en devellopant (x-2) ^3 .
Par contre si tu as la partie b du probleme je la veux bien :D

[Azarnok]

Par contre si tu as la partie b du probleme je la veux bien

Désolé je ne l'ai pas encore faite ....

[matelos90]

Est ce que tu pourras me l envoyer quand tu l aurs fait stp